Prepare Input Files

Follow the standard formatting used in the PDB files, but ensure that the following constraints are satisfied before uploading the PDB file into the server

1. The protein length should be between 50-500 amino acids.
2. The PDB file should not contain any hetero-atom or non-standard amino acids.
3. The PDB file should contain the complete description of heavy atoms (To model missing atoms, visit here)
4. The PDB file should contain one structural state (i.e. one model entry) in case of NMR structures.

 

If the uploaded file / PDB ID contains multiple chains, only the first chain entry will be considered by the server unless otherwise mentioned. The same holds true for the NMR models, where only the first model will be considered for the further predictions.

Upload PDB Files

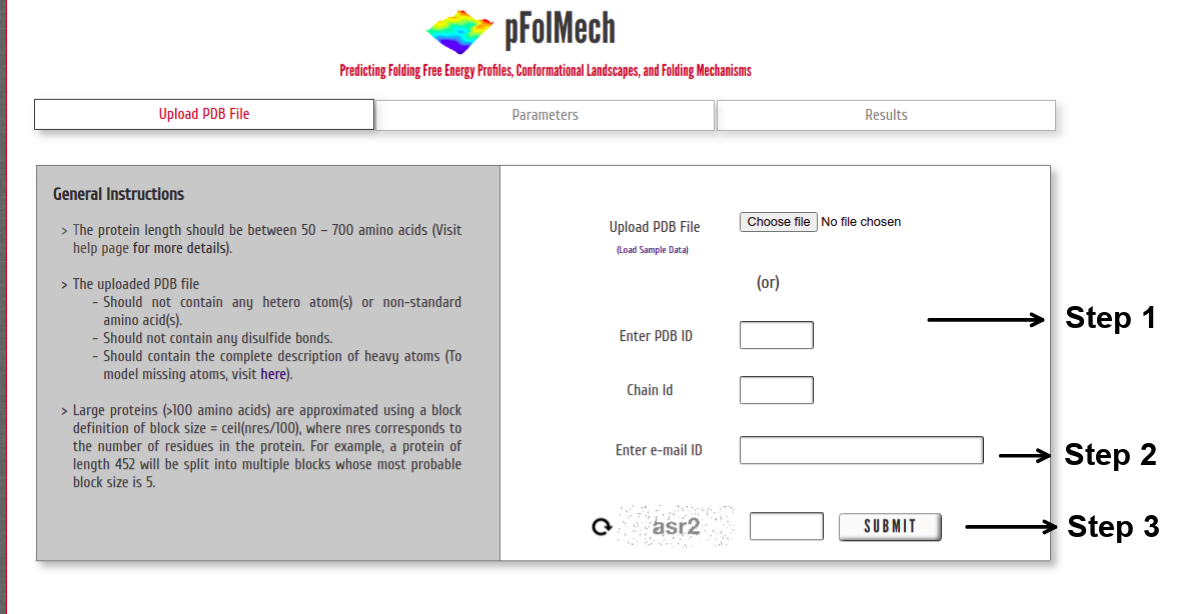Step 1: Upload the PDB file satisfying the above-specified considerations (or) Enter a valid PDB ID. (Optional) Specify chain ID of the protein to be considered.

 

Step 2: The model predictions from the server may take a few minutes to a few hours depending on the protein size (larger the protein, the more the number of microstates and hence a longer time is required). Providing an e-mail ID is required as some jobs might take longer to complete.

 

Step 3: Enter valid CAPTCHA and click on “SUBMIT” to proceed.

 

Specify Input Parameters

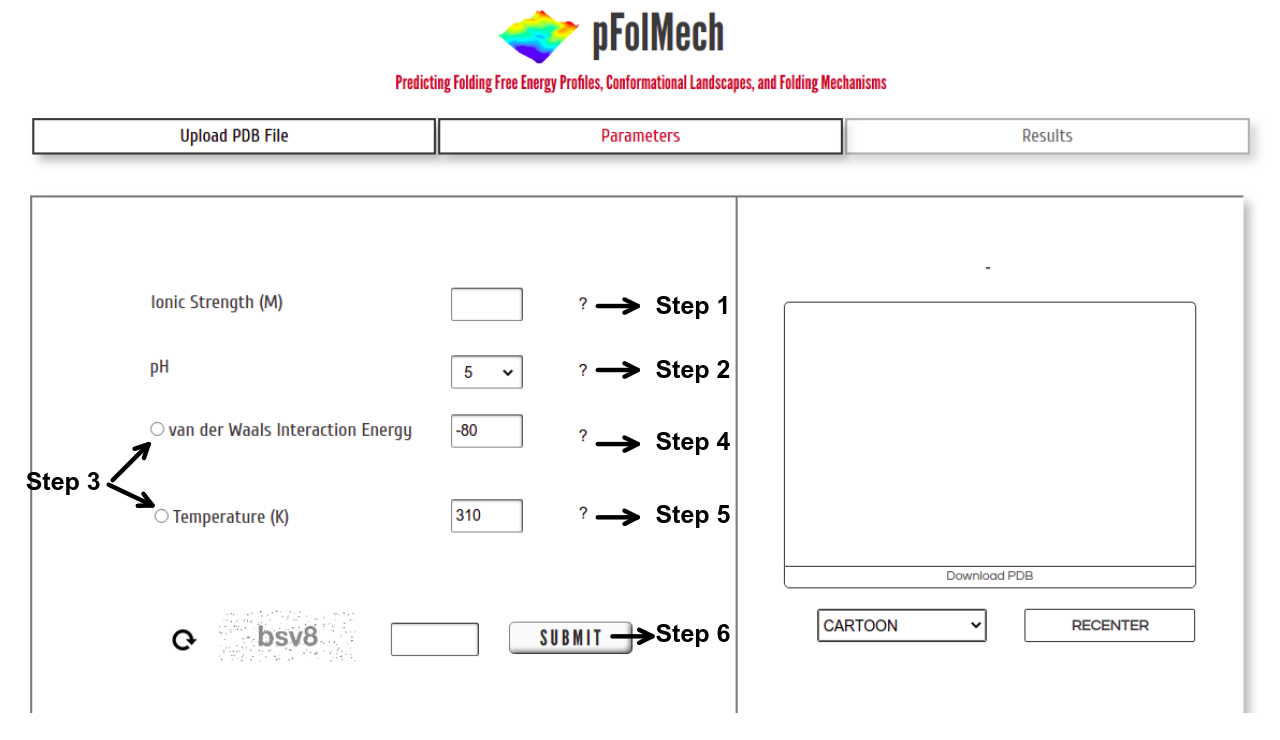Step 1: Enter a value of Ionic Strength within the range of 0.01 to 0.1 M.

 

Step 2: Choose a pH from the drop-down – options for only pH 5 or 7 are provided. At pH 5, histidine is additionally protonated.

 

Step 3: Either temperature or van der Waals interaction energy can be chosen to vary. The non-selected option is assigned a default value.

 

Step 4: Enter a value of van der Waals Interaction Energy within the range of -110 to -60 J mol^-1 per native contact. The default value is set at -80 J mol^-1 per native contact

 

Step 5: Enter a value of Temperature within the range of 273 to 343 K. The default value is set at 310 K.

Step 6: Enter valid CAPTCHA and click on “SUBMIT” to proceed.

Note : The MATLAB scripts used in the server are available in the associated GitHub repository. All parameters may be modified in these scripts (Gopi S et al., 2019; Naganathan AN et al., 2021). The scripts may generate NaN or Inf free energy values for certain large proteins or large negative van der Waal's interaction energies. This problem can be rectified by increasing the number of calculating windows (the parameter "wi" in the script FesCalc_Block.m).

Output

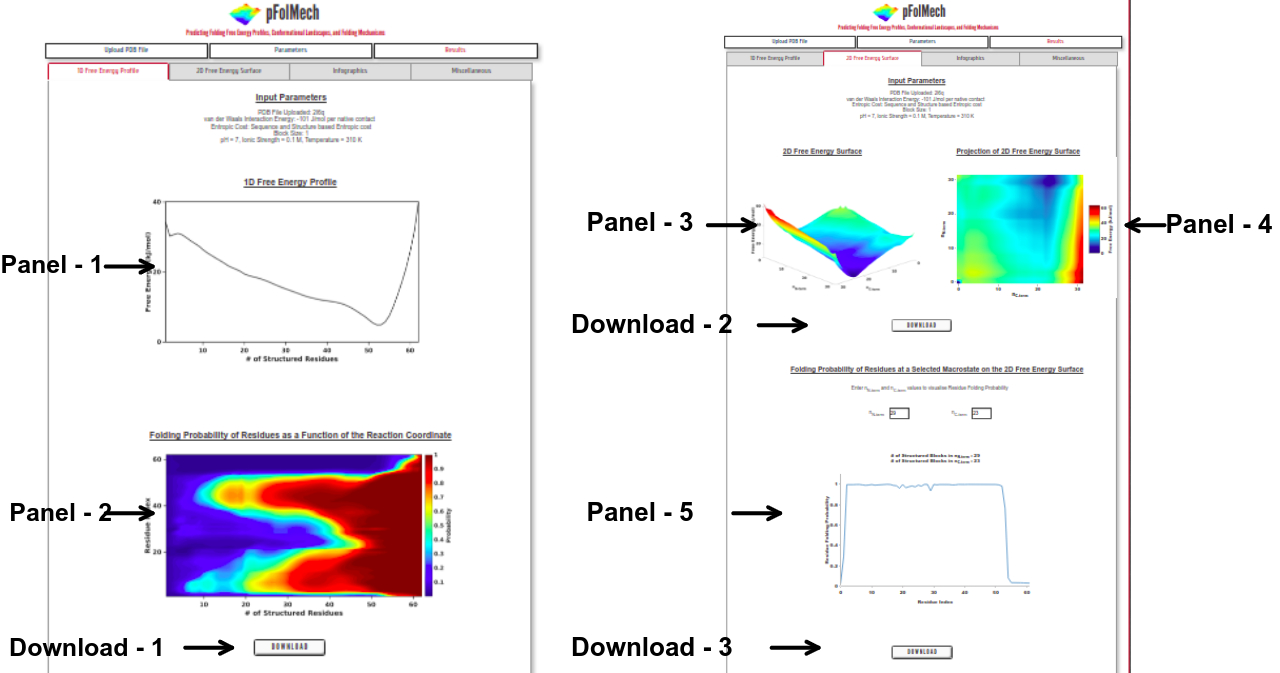
1D Free Energy Profile

Panel 1: The one-dimensional free energy profile of the protein as a function of the reaction coordinate, the number of structured residues or blocks.

 

Panel 2: The folding probability of each residue in the protein as a function of the reaction coordinate.

 

Download 1: Click on “DOWNLOAD” to save the output data files of Panel 1 and Panel 2 into your local machine.

 

2D Free Energy Surface

Panel 3: The two-dimensional free energy surface of the protein with the number of structured N- and C-terminal blocks (n_N-term and n_C-term , respectively) represented on the x- and y-axes and the free energy represented on the z-axis.

 

Panel 4: An interactive projection of the two-dimensional free energy surface as seen from above.

 

Download 2: Click on “DOWNLOAD” to save the output data files of Panel 3 and Panel 4 into your local machine.

 

Panel 5: The folding probability of each residue in the protein at user-specified macrostates on the two-dimensional free energy surface.

 

Download 3: Click on “DOWNLOAD” to save the output data files of panel 5 into your local machine.

 

 

 

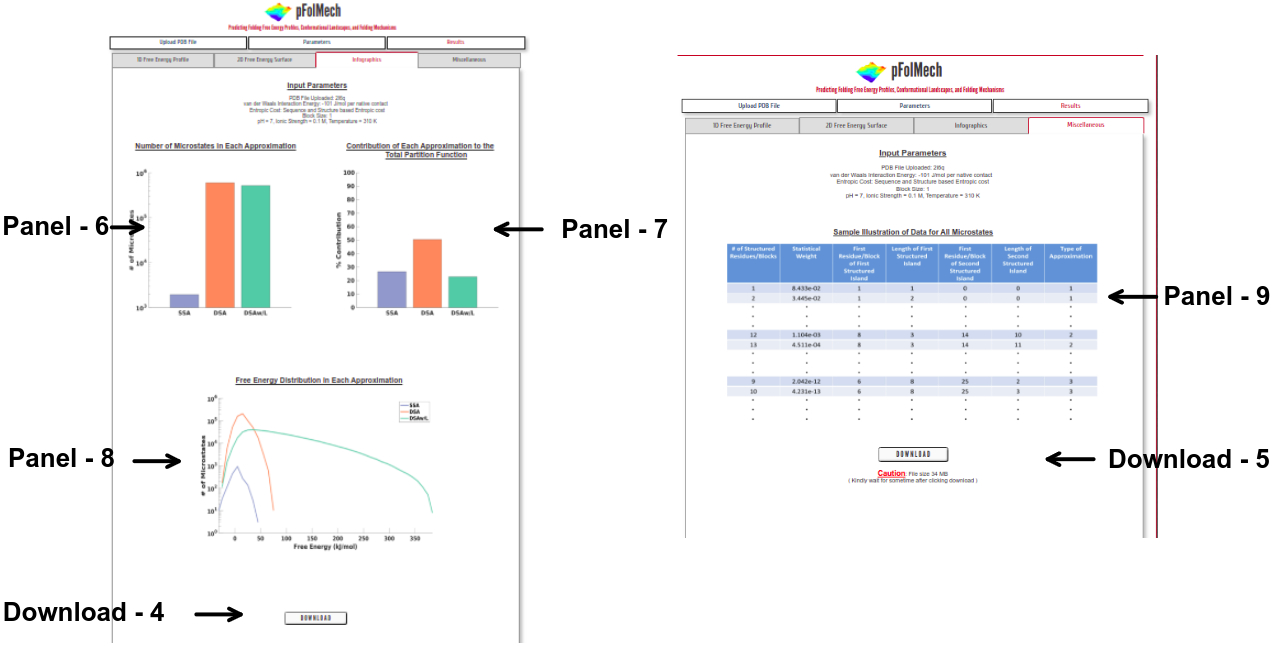
Infographics

Panel 6: The number of microstates considered for each of the approximations (SSA, DSA, and DSAw/L).

 

Panel 7: The percentage contribution of microstates from each of the three approximations to the total partition function.

 

Panel 8: The distribution of free energies among the microstates of each approximation.

 

Download 4: Click on “DOWNLOAD” to save the output data files of Panel 6, Panel 7 and Panel 8 into your local machine.

 

Miscellaneous

Panel 9: A representative visual showing the information on each microstate. This data is downloadable from this page.

 

Download 5: Click on “DOWNLOAD” to save the output data files into your local machine.

 

Structure-Based Statistical Mechanical Model

To predict the folding thermodynamics of the proteins at a residue-level resolution, we employ an extended version of the simple yet detailed Wako-Saitô-Muñoz-Eaton model. The WSME model incorporates multiple energetic terms like vdW interactions, electrostatics, solvation, and residue specific conformational entropy in its energy-entropy function. In this model, residues are assumed to sample two sets of conformations: folded (native) and unfolded (non-native) that are assigned the binary variables 1 and 0, respectively thus, leading to a total of 2N structured microstates or conformations for an N-residue protein.

The free energy of each microstate is

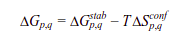
where the effective stabilization free-energy 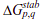of a particular microstate (p, q) (i.e., a string of 1’s between and including p and q) at a temperature T is represented as a sum of van der Waals interactions (EVdW), electrostatic potential (EElec) and solvation free energy (∆Gsolv). 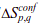accounts for the entropic cost or penalty for fixing residues between and including p and q in the native conformation. Further details on the model and equations to calculate the folding probability of residues can be found in the literature (Wako H & Saitô N, 1978; Muñoz V & Eaton WA, 1999; Naganathan AN, 2012; Naganathan AN & Kannan A. 2021).

The version of the WSME model used in this server, called the bWSME model, employs an approximation that treats multiple consecutive residues (max. of 5) as a single block. The number of residues condensed into a block depends on the protein length. Three further approximations are used in place of considering all 2N microstates. The single sequence approximation (SSA) includes those microstates that involve a single island of contiguous structured structured blocks/residues. Similarly, the double sequence approximation (DSA) considers microstates with two structured islands with intervening unfolded residues. The DSAw/L is identical to DSA in terms of the microstate description but additionally accounts for interactions between two structured islands if they interact in the folded state. The number of microstates used in each approximation may be calculated, employing the binomial coefficient, to be 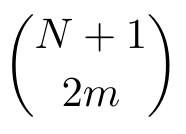, where N is the number of blocks and m is the sequence approximation. These approximation allows for the study of much larger proteins with limited computational resources. The performance of the bWSME model has been validated against experimental observables for proteins of varying lengths (Gopi et al., 2019).

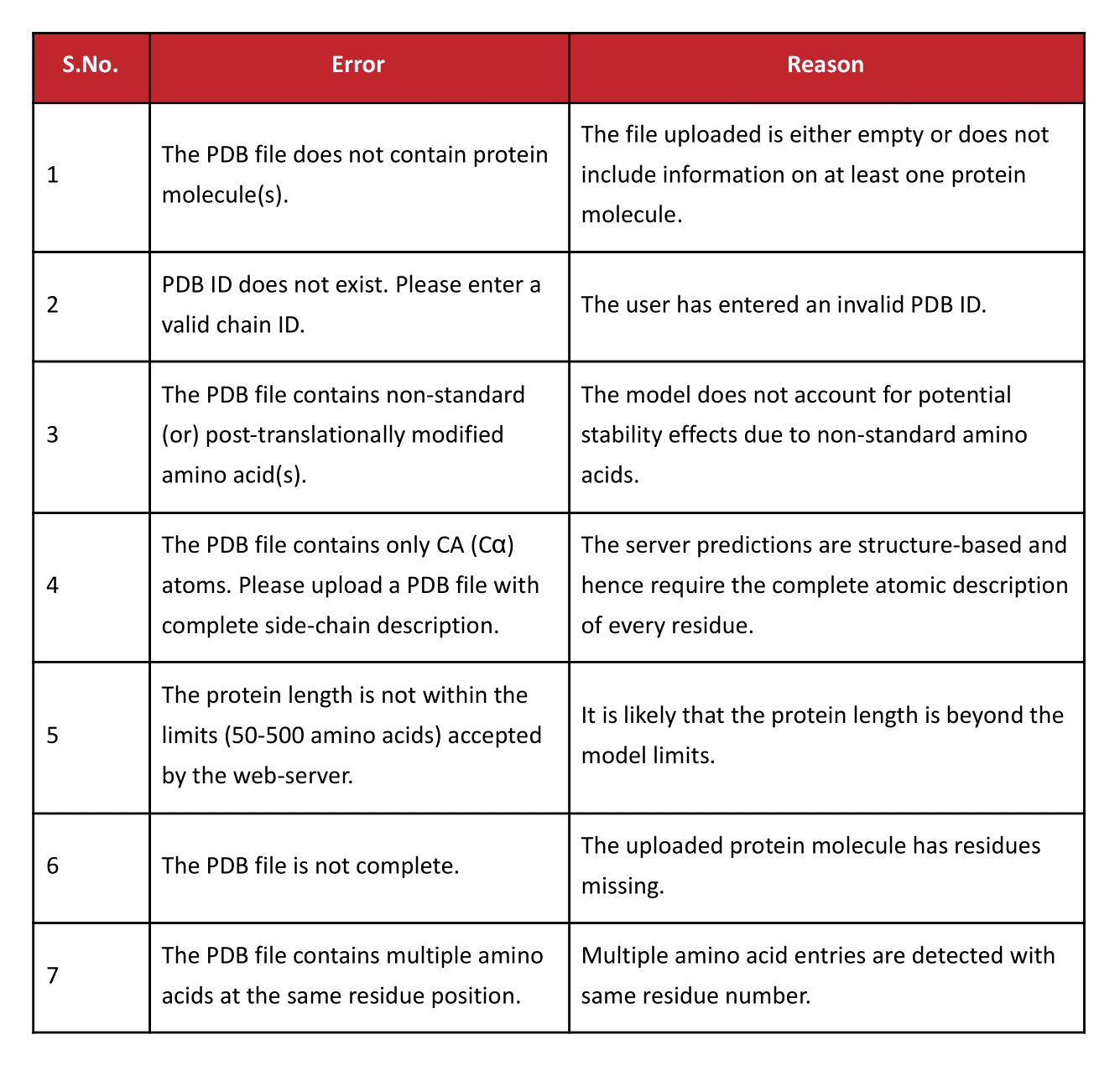
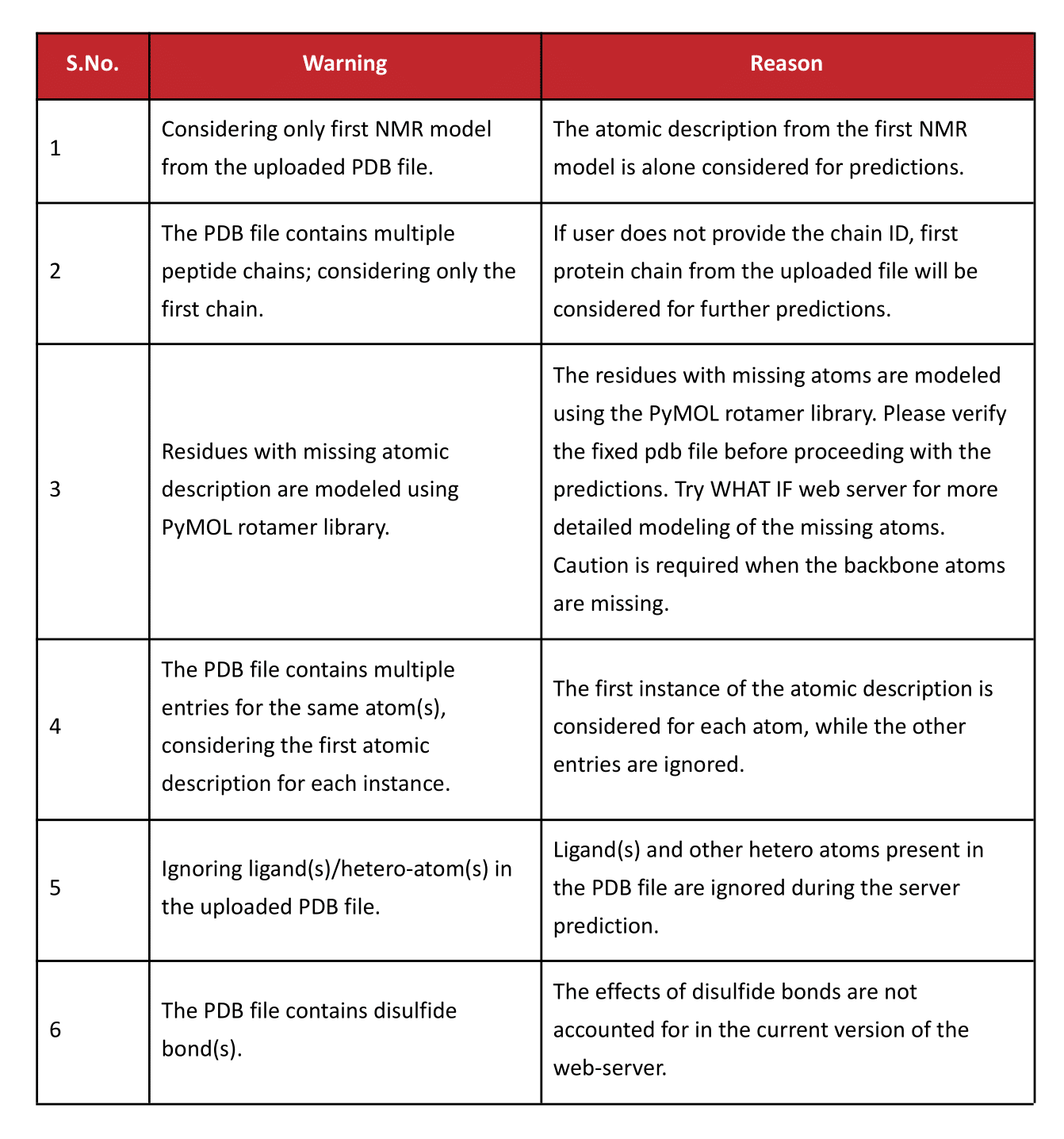
Errors and Warnings

Further Reading

1. Wako, H.; Saito, N. Statistical Mechanical Theory of Protein Conformation 0.2. Folding Pathway for Protein. J. Phys. Soc. Jpn. 1978, 44, 1939−1945. 

 

2. Muñoz, V.; Eaton, W. A. A Simple Model for Calculating the Kinetics of Protein Folding from Three-Dimensional Structures. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 11311−11316. 

 

3. Naganathan, A.N. Predictions from an Ising-Like Statistical Mechanical Model on the Dynamic and Thermodynamic Effects of Protein Surface Electrostatics. J. Chem. Theory Comput. 2012, 8, 4646-4656. 

 

4. Naganathan, A. N. A Rapid, Ensemble and Free Energy Based Method for Engineering Protein Stabilities. J. Phys. Chem. B. 2013, 117, 4956−4964. 

 

5. Rajasekaran, N.; Gopi, S., Narayan, A.; Naganathan, A. N. Quantifying Protein Disorder through Measures of Excess Conformational Entropy. J. Phys. Chem. B. 2016, 120(19), 4341-4350. 

6. Gopi, S., Aranganathan, A., & Naganathan, A. N. (2019). Thermodynamics and folding landscapes of large proteins from a statistical mechanical model. Current Research in Structural Biology, 1, 6–12. 

7. Naganathan, A. N., & Kannan, A. (2021). A hierarchy of coupling free energies underlie the thermodynamic and functional architecture of protein structures. Current Research in Structural Biology, 3, 257–267. 

8. Naganathan, A. N., Dani, R., Gopi, S., Aranganathan, A., & Narayan, A. (2021). Folding Intermediates, Heterogeneous Native Ensembles and Protein Function. J. Mol. Biol., 167325.